|
Théorie des poutres ICAB Force/CR |
|
documentation ICAB > manuel de référence
Accueil > theorie des poutres
|
Ce chapitre résume brièvement les hypothèses et les théorèmes utilisés en résistance des matériaux pour la modélisation de structures utilisant des poutres.
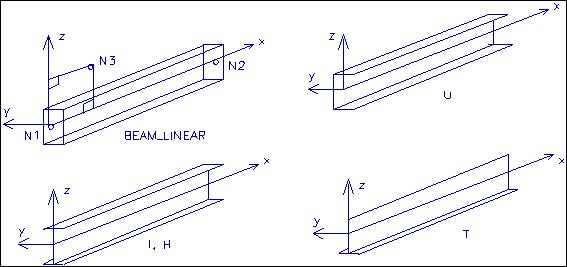
En termes non mathématiques, une poutre est un solide élancé dont une dimension, la longueur, est très supérieure aux deux autres. Cette particularité permet de simplifier l'étude mécanique d'une poutre par apport à celle d'un corps solide quelconque. La section d'une poutre est défini par le plan perpendiculaire à la direction de l'élancement.
Dans le repère local de la poutre, nous notons (x) la direction axiale et (y,z) les directions définissant les deux axes de la section de la poutre. Par convention, l'axe (z) correspond à la direction définissant la plus forte inertie. Ainsi pour une poutre en I, l'axe (z) sera l'axe parallèle à l'âme, l'axe (y) sera parallèle aux semelles.

Quels que soient les sollicitations appliquées à une poutre, la section reste plane et son aire est constante.
Il est donc possible de définir le déplacement d'un point quelconque d'une section à partir de trois déplacements (u, wy, wz) et trois rotations (rx, ry, rz).
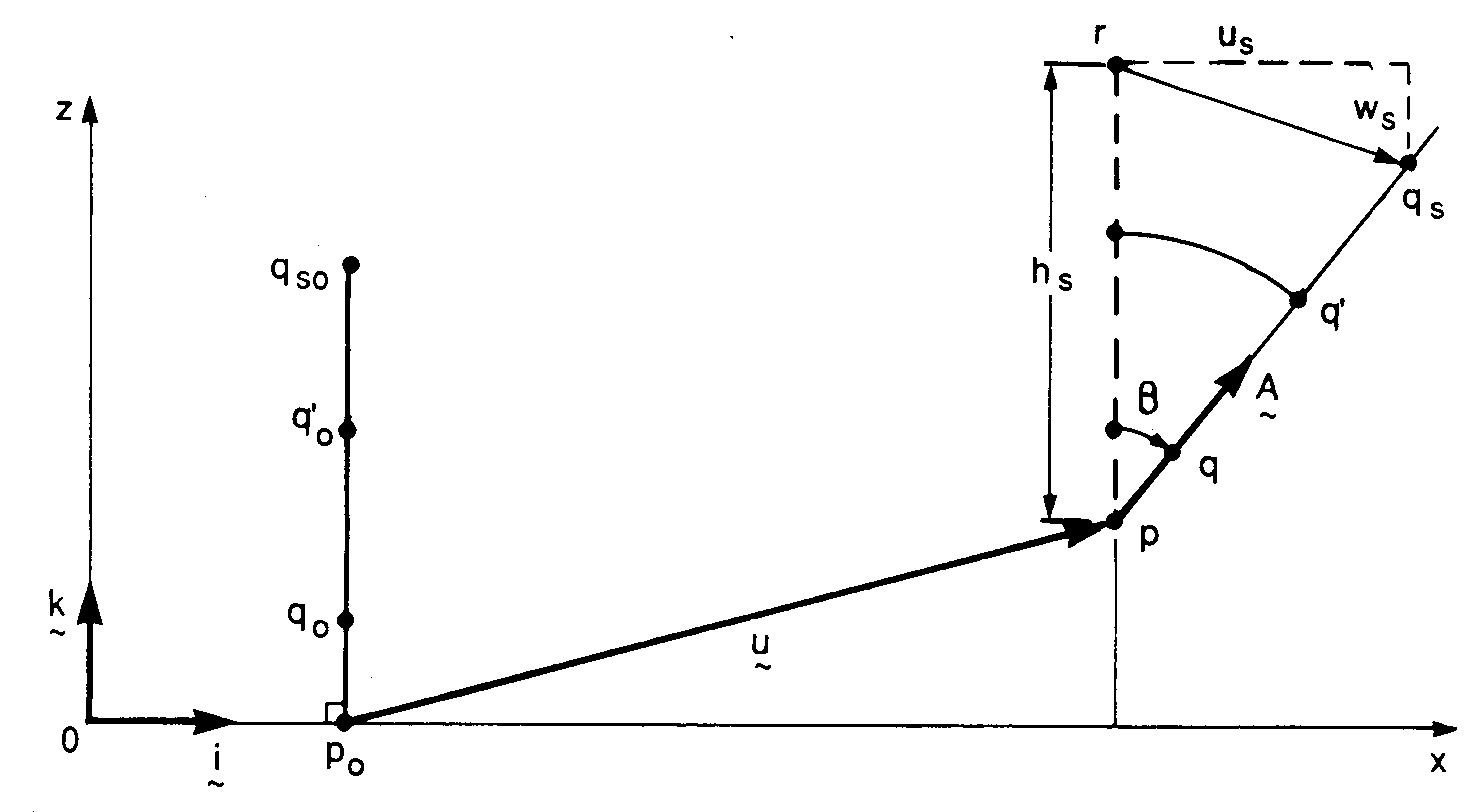
Les déplacements u, wy et wz sont les translations du point de la section sur l'axe (x) local de la poutre. La valeur qx (respectivement qy, qz) est la rotation de la section autour de l'axe x (respectivement y, z) local de la poutre.
Les déplacements (Ux, Uy, Uz) dans le repère local de la poutre pour un point de la section situé aux coordonnées <r>=(x, y, z) sont au premier ordre (cos(a)=1+o(2)»1, sin(a)=a+ o(3) ):
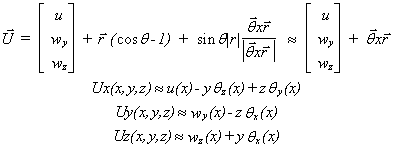
Les déformations sont:
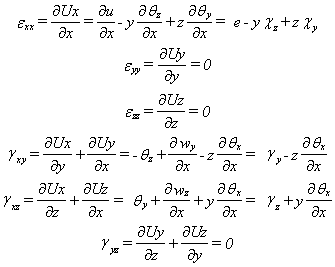
Avec:
Nous adoptons la notation U,x pour désigner la dérivée première de la grandeur U par rapport à la variable x.
Les hypothèses de modélisation des poutres simplifient le tenseur des contraintes.
Les hypothèses de modélisation des poutres font l'assertion que les contraintes de striction sont nulles syy = szz = 0, ainsi que la contrainte de cisaillement Tauyz =0. Il s'agit de l'hypothèse des contraintes planes dans l'épaisseur de la poutre. Notez que la théorie des poutre pose la double hypothèse des contraintes planes et des déformations planes (induites par l'hypothèse des sections droites eyy= ezz=Gammayz=0). Ces hypothèses ne sont pas compatibles simultanément: il s'agit d'approximations.
La contrainte normale sxx est souvent simplement notée s. Les efforts résultants sont l'effort normal Nx, les efforts tranchants Ty, Tz, le moment de torsion Mx et les moments fléchissants My, Mz à partir de l'intégration surfacique des contraintes sur une section à une abscisse (x) donnée.
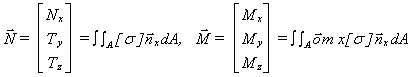
Soit encore:
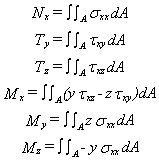
Les équations d'équilibre de mécanique des milieux continus sont, pour un volume V de densité r en accélération {a} soumis à un état de contrainte [s subissant des forces externes volumiques {fv} et surfaciques {fS}:
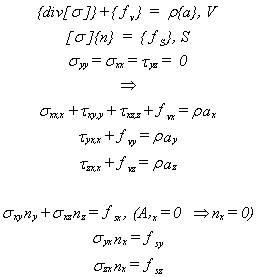
Pour une analyse statique, les forces volumiques d'accélérations sont nulles ({a}=0). Pour une poutre, les contraintes syy, szz, tyz sont nulles. En intégrant ces relations d'équilibre sur une section A, l'équilibre des forces et des moments pour une section de la poutre s'écrit:

Les forces et moments linéiques qui résultant des forces externes volumiques et surfaciques sont notés fx, fy, fz, mx, my, mz (les moments linéiques seront supposés nuls dans la suite de ce manuel):
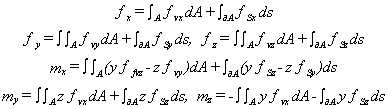
Dans ICAB Force, les forces externes linéiques sont créées par la gravitation et les charges réparties.
Si la poutre est constituée d'un matériau élastique, alors les relations entre les contraintes et les déformations sont:
| sxx = Ex exx | Ex est le module d'Young dans la direction x de la poutre |
| txy = Gxy.Gammaxy | Gxy est le module de cisaillement xy |
| txz = Gxz.Gammaxz | Gxz est le module de cisaillement xz |
Si le matériau est isotrope alors Gxy = Gxz = G = E/(2+2nu) où nu est le coefficient de Poisson.
En intégrant les relations entre contraintes et déformations sur l'aire de la section de la poutre, nous obtenons:
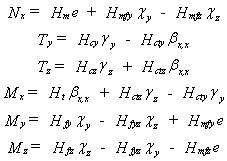
Les grandeurs associées au module d'Young sont:
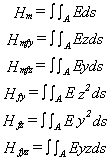
Les grandeurs associées aux modules de cisaillement sont:
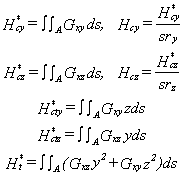
Ht* est la rigidité de torsion pour une section non soumise à un gauchissement, par exemple pour un tube circulaire.
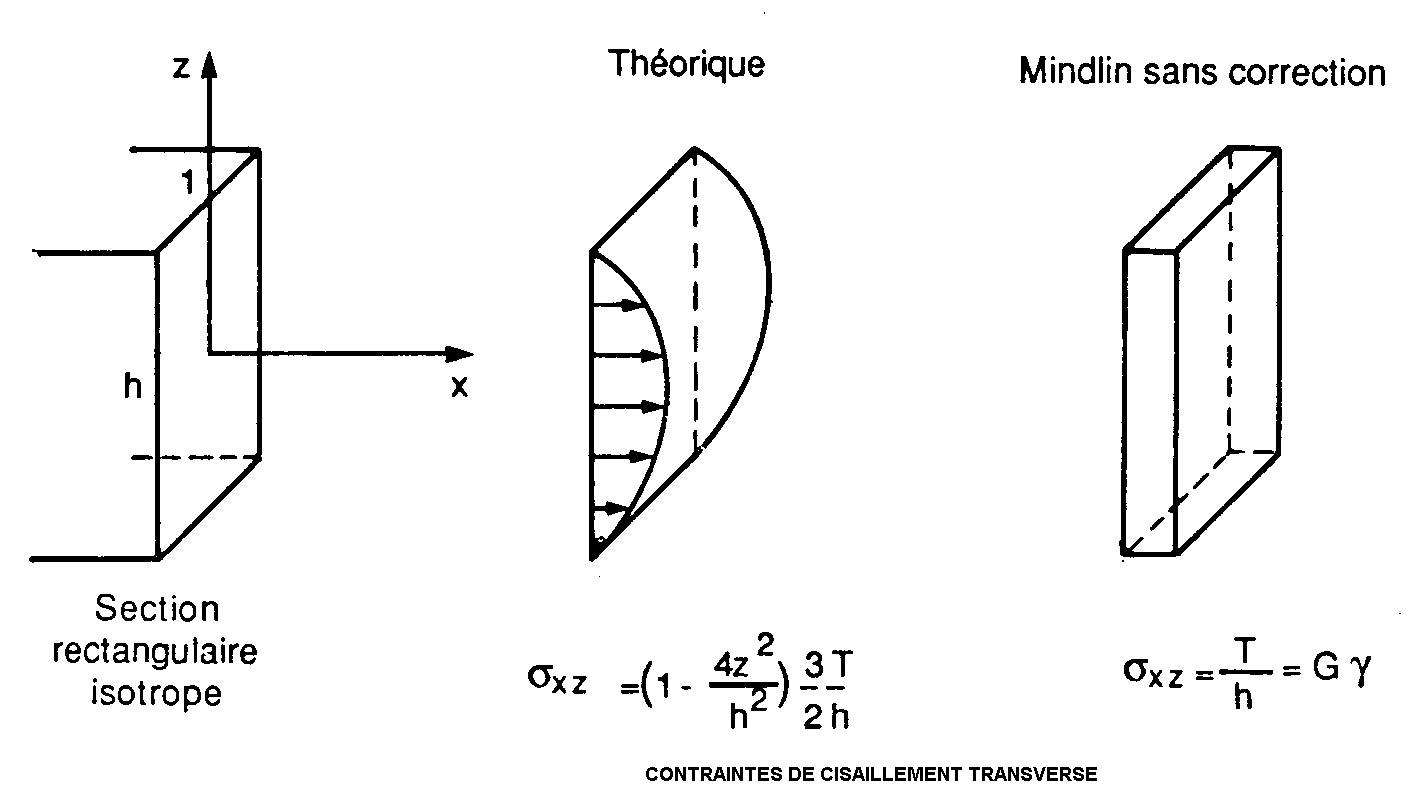
Les rigidités marquées d'une étoile dans les intégrales ci-dessus sont calculées directement à partir de la première hypothèse fondamentale (sections droites, cf équation(1)). Mais cette hypothèse n'est pas compatible avec les équations d'équilibre que doivent satisfaire les contraintes. En effet, la cinématique simplifiée des sections de poutres impliquent que les déformations de cisaillement transverse ?y et ?z soient constantes à travers l'épaisseur. Dans ce cas, les contraintes de cisaillement ne peuvent être nulles sur la peau extérieure de la poutre. Or, pour une poutre réelle, ces contraintes sont nulles ([s].n = 0, pour tout vecteur n normal à la peau extérieure).
Les coefficients H*cy et H*cz majorent les rigidités réelles de cisaillement transverse. Les coefficients sans dimension sry et srz introduisent des corrections sur les rigidités de cisaillement transverse. Le coefficient de Reissner k=1/sr est défini de façon à ce que l'énergie interne U1 de déformation de cisaillement transverse associée à la distribution exacte de t exacte et l'énergie U2 associée au modèle simplifié soient identiques:
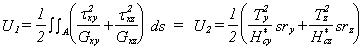
Voici quelques exemples de valeurs des coefficients correctifs de rigidité sr (Shear area Ratio) définis comme ci-dessus:
| section pleine rectangulaire | 6/5 |
| section circulaire | 7/6 |
| tube circulaire | 2 |
| tube carré | 2.4 |
Négliger l'effet des cisaillements transverses revient à prendre sry=srz=0 (formulation de Kirchhoff, par opposition à la formulation de Timoshenko qui prend en compte les cisaillements transverses). A partir de considérations dynamiques (identification de k à partir de l’expresson d’une fréquence propre fondamentale) le coefficient dit de Mindlin est k=pi2/12=1/1.216. L'effet des cisaillement transverses est d'autant plus faible que la longueur de la poutre (L) est grande par rapport au rayon de giration (i). Dans le cas d'une poutre de longueur L, de section rectangulaire de hauteur h constituée d'un matériau homogène, le coefficient Phi qui caractérise l'influence des déformations de cisaillement transversal tend vers zéro en (h/L)2:
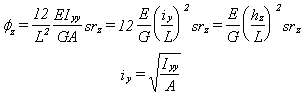
Une correction également fondée sur des considérations énergétiques peut être menée pour la rigidité de torsion. La correction tient compte du gauchissement de la section sous l'effet de la torsion. Le coefficient H*t majore la rigidité de torsion réelle Ht.
Soit une poutre de longueur L rotulée à ses extrémités et soumise à une charge linéique uniforme p (cf Timoshenko I, p. 166). La flèche au centre est:
![]()
Pour srz=0, nous retrouvons l'expression de la flèche de la poutre élancée. Lorsque le coefficient srz est non nul, la flèche est plus importante: la prise en compte des effets du cisaillement transverse avec le coefficient srz permet d'éviter le blocage en cisaillement des poutres courtes.
Pour une poutre horizontale en porte-à-faux soumise à son extrémité à une force verticale, la flèche comporte encore un terme linéaire en L associé au cisaillement et un terme cubique associé à la flexion:
![]()
N.B. Un cisaillement constant pur ne peut engendrer qu'une flèche variant linéairement, alors qu'une flexion constante pure crée une courbure et donc une flèche variant au moins de façon quadratique mais sans terme linéaire.
Les formules des deux exemples ci-dessus sont établies pour des poutres dont les axes locaux sont principaux et passent par l'axe neutre.
Comme indiqué ci-dessus, l'hypothèse des sections droites implique des déformations de cisaillement transverse Gammaxy, Gammaxz constantes à travers l'épaisseur. En conséquence, les contraintes de cisaillement Tauxy Tauxz ne respectent pas les conditions aux limites sur les faces supérieures et inférieures, ainsi que les équations locales d'équilibre dans la direction x de l'axe de la poutre.
Prenons une poutre soumise à une flexion autour de l'axe y exclusivement et non soumise à une force volumique. Nous conservons l'hypothèse des sections droites pour le calcul des déformations axiales (linéaires selon z). Pour déterminer la répartition des contraintes de cisaillement transverse, reprenons les équations d'équilibre statique:
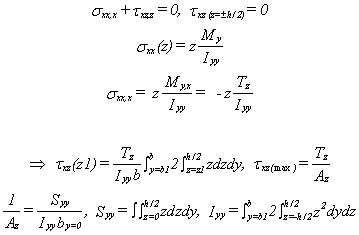
L'aire cisaillée Az fait intervenir le moment statique Syy, le moment d'inertie Iyy et la largeur de la section b (cf CM66 3,31 ou Timoshenko I, p 112). Par exemple, pour une section rectangulaire dont l'aire est A = b.h, on tire txz (max) = 3/2 Tz/A. La distribution de contrainte de cisaillement txz est parabolique dans l'épaisseur.
L'expression de la contrainte maximale de cisaillement transverse peut s'écrire txz (max)=Tz/Az. Cet état de contrainte est atteint sur la fibre neutre pour des poutre symétriques. Timoshenko utilise ce coefficient Az, dit "aire cisaillée équivalente", pour définir le coefficient correctif de rigidité srz = A/Az pour la prise en compte des cisaillements transverses. Notez que le rapport A/Az est différent du coefficient de Reissner défini ci-dessus qui représente au mieux l'énergie de déformation. Toutefois, ces coefficients sont souvent relativement proches, en particulier pour des profilés laminés.
La torsion d'un profil se produit en général avec un gauchissement w tel que:
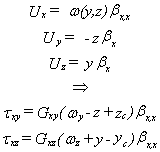
Effet du gauchissement sur poutre en I:
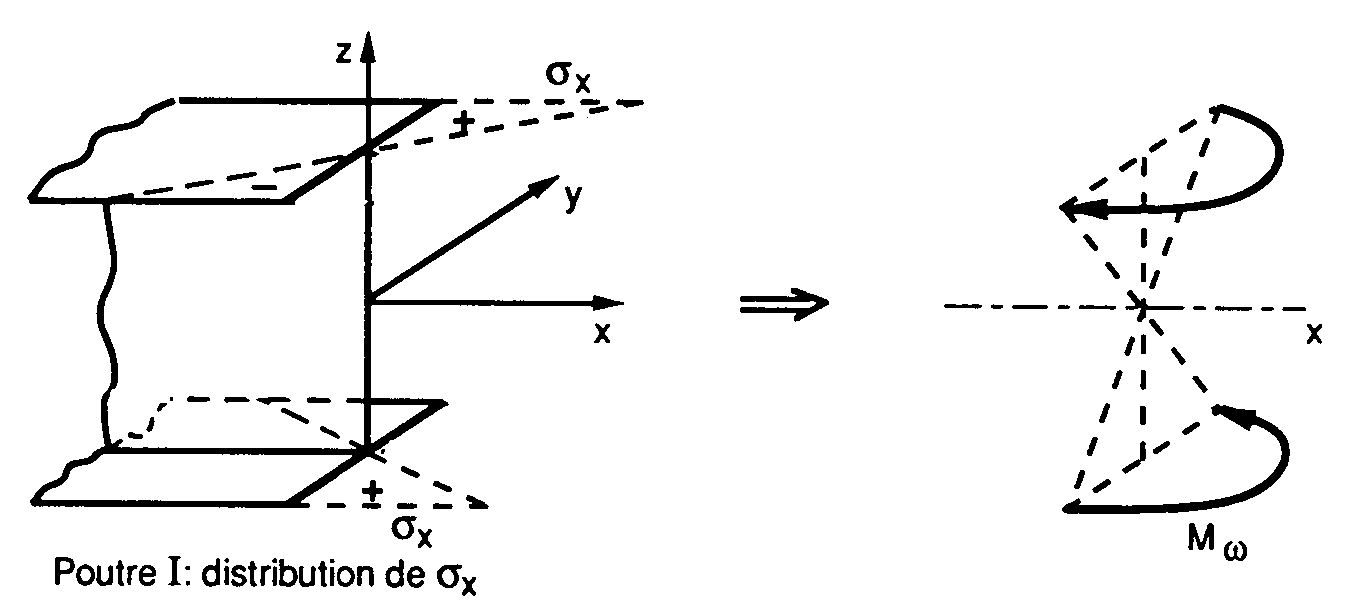
Le centre de torsion (yc, zc) est défini de manière à ce qu'un effort tranchant Ty ou Tz ne produise aucune torsion; soit encore, qu'une torsion ne crée pas de flèche. Les équations d'équilibre conduisent à:
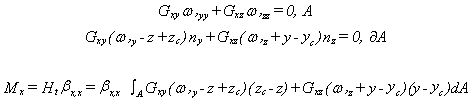
Pour une section rectangulaire homogène d'épaisseur e petite par rapport à la hauteur, le moment de torsion est approximativement:
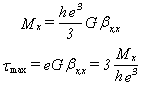
Pour les profilés de faible épaisseur comme les poutres en I, U, les cornières, ce calcul peut être repris en considérant ces profilés comme un assemblage de sections rectangulaires. Toutefois, des concentrations de contraintes apparaissent aux raccords entre les ailes et l'âme. Le coefficient K de concentration de contrainte amplifie la contrainte moyenne (cf Timoshenko II, p.295).
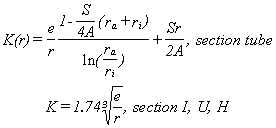
Pour les profils I, H, U, le coefficient K fait intervenir l'épaisseur e de l'aile et le rayon r de raccordement entre l'âme et l'aile. Pour les tubes présentant des angles rentrant (comme un tube carré), le coefficient K fait intervenir les rayons interne ri et externe ra, l'aire A et le périmètre moyen S de la section.
Pour une section quelconque à paroi mince d'épaisseur e, de longueur totale S de la ligne de courbe moyenne et d'aire A contenue à l'intérieur de la ligne moyenne:
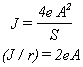
Les calculs menés pour des poutres de section constante ne sont pas rigoureusement applicables aux poutres de section variable. En effet, des concentrations de contraintes apparaissent lorsque la section de la poutre varie brusquement.
Par exemple, pour un arbre circulaire comportant une rainure hyperbolique de plus petit rayon r et de diamètre d, le coefficient de contrainte pour une flexion simple peut être approché par la formule K=0.75(d/2r)0.5 lorsque d >> 2r (cf Timoshenko II, p.304).
Les moments de flexion sont calculés par rapport à l'axe neutre dans le repère local principal et le moment de torsion par rapport au centre de torsion (Il est supposé que l'axe de neutre coincide avec l'axe de torsion).
Si le repère local n'a pas pour origine l'axe neutre, la position de l'axe neutre (y0, z0) est calculé de manière à ce que les rigidités de couplage membrane-flexion soient nulles:
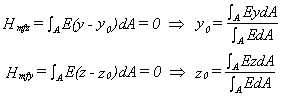
Nous supposons maintenant que le repère local a pour origine l'axe neutre. Si le moment d'inertie de couplage Hfyz n'est pas nul, une rotation a des axes permet d'éliminer ce terme de couplage entre les flexions (y) et (z):
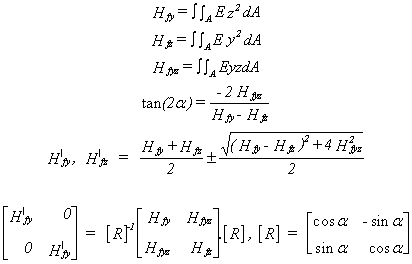
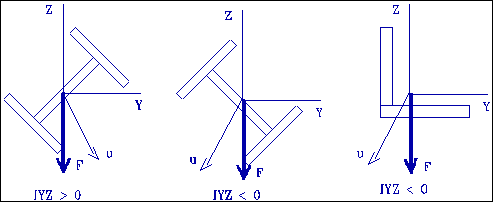
Pour les poutres constituées d'un matériau isotrope homogène comme l'acier, les rigidités sont calculées à partir d'intégrales sur la section où seules les caractéristiques géométriques interviennent.
Si les moments d'ordre 1 sont nuls, ce qui est le cas si les calculs sont réalisés à partir de l'axe neutre, nous avons:
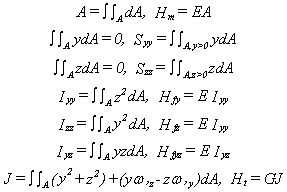
Ces coefficients sont l'aire A, les moments statiques Syy, Szz, les moments d'inertie Iyy, Izz et le moment de torsion J. Les efforts résultants sont donc:
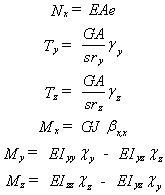
Il est toujours possible de choisir un repère dans le plan de la section (yz) de façon à ce que Iyz soit nul. Dans ce cas, les axes (y) et (z) sont les axes principaux d'inertie de la section de la poutre.
Le comportement de la poutre est donc simplement caractérisé par:
- deux coefficients portant sur les matériaux (E et G=E/(2+2nu), où nu est le coefficient de Poisson). Pour l'acier utilisé couramment dans les constructions métalliques E=210x109 Pa, n=0.3,
- six coefficients caractéristiques de la géométrie A (aire de la section), Iyy, Izz (moments d'inertie), J (constante de torsion éventuellement corrigée telle que J < J*), sry, srz (coefficients de correction de l'aire cisaillée).
Les paramètres de l'entité PROPERTY(TYPE=ISOTROPIC) qui définissent le matériau sont E=E, NU=n. G est défini comme G = E/(2+2n).
Les paramètres de l'entité PROPERTY(TYPE=BEAM_LINEAR) qui définissent les propriétés physiques sont AR=A, IYY=Iyy, IZZ=Izz, TC=J, SRY=sry, SRZ=srz.
Par intégration à partir des relations contraintes/déformations indiquées dans les sections précédentes, les relations efforts résultants F (N, Ty, Tz, Mx, My, Mz) aux extrémités d’une poutre s’expriment en fonction des déplacements q à ces mêmes extrémités.
Pour une poutre de section droite sans excentration de fibre neutre ni de centre de torsion, les axes locaux étant principaux, la matrice de rigidité élémentaire d’une poutre à deux nœuds telle que F=K.q est :
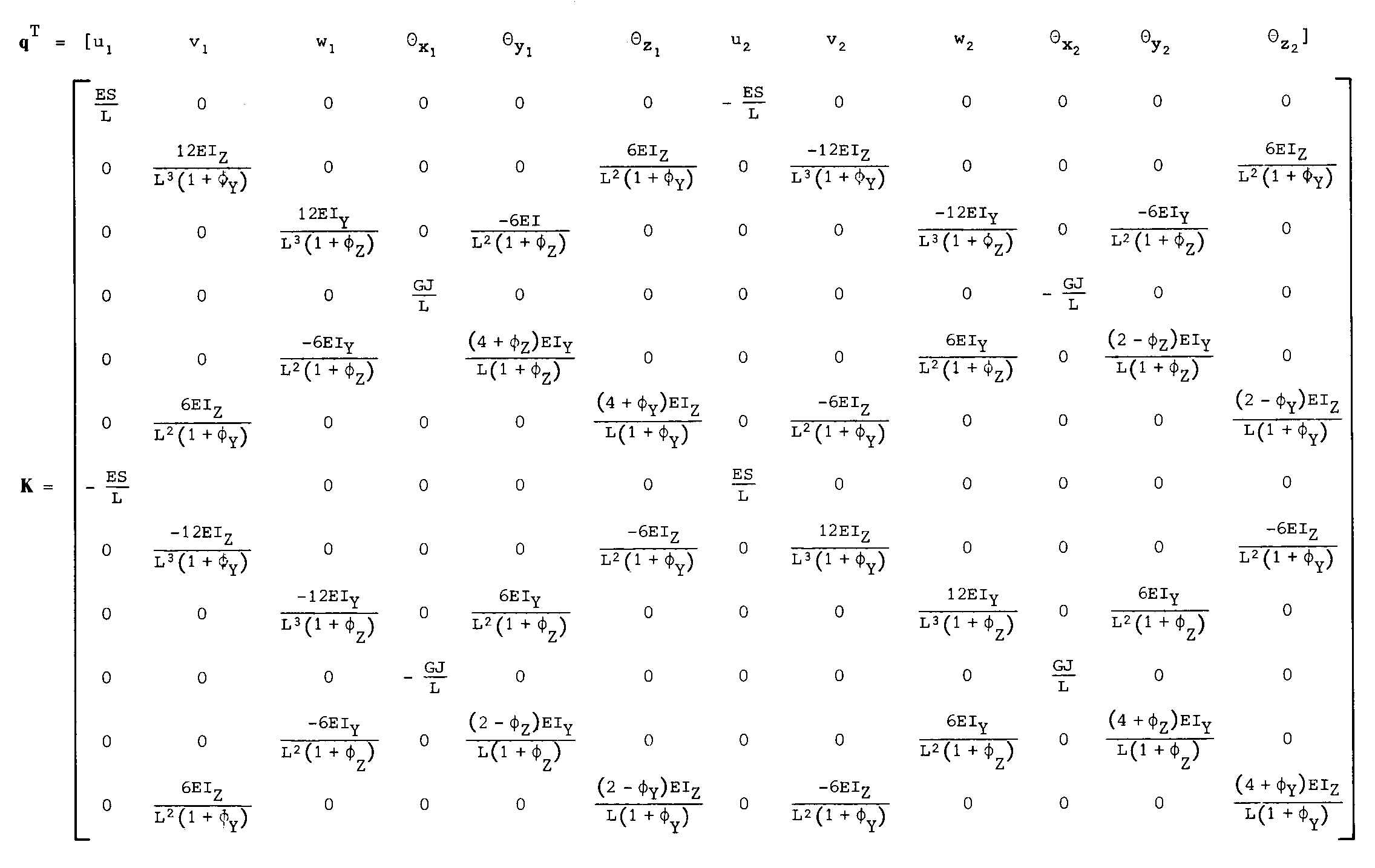
Lorsqu'une poutre est précontrainte, la relation entre efforts résultants et déformations fait intervenir ces précontraintes.
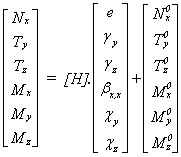
La matrice [H] contient les termes de rigidité définis dans les sections précédentes.
Les efforts de précontraintes en tension Nx et moments (My, Mz) dans une poutre correspondent aux efforts initiaux dans la poutre lorsque la poutre est encastrée à ses extrémités. Si les extrémités sont libres, une tension initiale Nx>0 produira un raccourcissement de la poutre; un moment initial Mz>0 produira une flèche positive.
Efforts tranchants de précontrainte: si les moments fléchissants ne sont pas équilibrés, un effort tranchant est introduit pour assurer l'équilibre de la poutre:
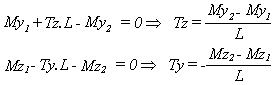
ATTENTION: une poutre précontrainte ne peut être fractionnée en plusieurs tronçons. Si tel est le cas, chaque tronçon est précontraint.
Nous notons a le coefficient de dilatation thermique du matériau de la poutre dans le sens de l'axe (x), DT = (T-Tref) l'écart de température par rapport à la température de référence pour laquelle les dilatations thermiques sont nulles. Nous avons:
e0xx = a.DT, Gamma0xy=0, Gamma0xz=0
s0 = -E e0xx, s0xy=0, s0xz=0
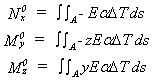
Les moments fléchissants sont créés par un gradient thermique dans le sens (y) ou (z) de l'épaisseur de la poutre. ICAB Force ne prend pas en compte les gradients thermiques dans le sens de l'épaisseur.
Pour les poutres de section circulaire creuse (CHS), le chargement d’un fluide sous pression est calculé de la manière suivante :
![]()
avec :
La contrainte de membrane due à la pression interne dans le tube est :
![]()
avec :
Par ailleurs, le fluide sous pression crée un effet de fond aux extrémités du tube, c’est-à-dire une poussée calculée à partir de la pression moyenne dans le tube :
![]()
Le poids du fluide crée également une charge linéique égale à:
![]()