TYPE=propriété_chaîne

chaîne de caractères indiquant le type de propriété. La liste des type de propriété est détaillée ci-dessous.

Liste des types de matériaux.

Liste des types de propriétés physiques.

MAT=matériau_{entier ou pointeur}

numéro ou pointeur du matériau qui doit être utilisé par défaut pour une propriété physique. Les caractéristiques de ce matériau seront utilisées par défaut lorsque le matériau n'est pas indiqué dans une entité ELEMENT. Ce paramètre ne peut être employé que pour les propriétés physiques et il est optionnel.

label_chaîne

nom de la propriété pouvant être utilisé comme pointeur.

TYPE=ISO
matériau isotrope

E=module, NU=poisson, DEN=_, A=a, ...;

Caractéristiques mécaniques

E=module_réel

Module d'élasticité dit module d'Young (Modulus of elasticity, Pa=N/m²)

NU=u_réel

coefficient de Poisson (Poisson's ratio)

G=g_réel

module de cisaillement (Shear Modulus, Pa), utilisé si NU n'est pas défini.

La loi de comportement d'un matériau élastique isotrope est rappelée ci-dessous:

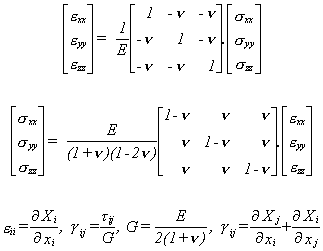
DEN=r_réel

densité massique (Mass density, kg.m-3)

A=a_réel

coefficient de dilatation thermique (Coefficient of thermal expansion).

La dilatation thermique résultant d'une différence de température dT entre la température de la structure et la température de référence (pour laquelle il n'y a pas de dilatation) est: e = a. dT.
La température de référence est définie dans une entité "LOAD(TYPE=AM_TEMPERATURE)"

GE=ge_réel

amortissement structurel (Structural element damping coefficient)
L'amortissement structurel introduit un terme complexe dans la matrice du module d'élasticité tel que le module complexe soit [E*] =  ( 1 + i .ge).[E]

Caractéristiques thermiques

KTC=k_réel

conductivité thermique (Thermal conductivity)

CP=cp_réel

chaleur spécifique (Specific heat)

Q=q_réel

taux de génération de chaleur (Heat Generation rate)

CF=cf_réel

coefficient de chaleur convective (Convective Film coefficient)

TC=tc_réel

capacité thermique par unité de surface (Thermal Capacity for unit area)

HF=hf_réel

taux de dégagement de chaleur (Heat Flux rate)

SHF=s_réel

taux de dégagement de chaleur surfacique (Surface Heat Flux rate)

AF=af_réel

facteur d'aire (Area factor)

EM=em_réel

émissivité (Emissivity)

AB=ab_réel

absorbtion (Absorbivity)

TREF=tr_réel

température de référence (Thermal expansion reference temperature)

Caractéristiques de mécanique non-linéaire et de rupture

MU=h_réel

coefficient de friction (coefficient of friction)

V=m_réel

viscosité (viscosity)

YS=s0_réel

contrainte de plastification (Yield stress), utilisée comme limite d'élasticité dans le calcul des critères de ruine pour les constructions métalliques (unité SI: Pa=N/m2)

SC=sc_réel

coefficient de gonflement (Swelling coefficient)

XT=s1+_réel

contrainte en traction X (Allowable stress in tension in X direction)

XC=s1-_réel

contrainte en compression X (Allowable stress in compression in X direction)

YT=s2+réel

contrainte en traction X (Allowable stress in tension in Y direction)

YC=s2-_réel

contrainte en compression X (Allowable stress in compression in Y direction)

S=t0_réel

contrainte en cisaillement plan (Allowable in-plane shear stress)

F12=f12_réel

terme d'interaction pour le critère de Tsai-Wu (Interaction term for Tsai-Wu)

TYPE=ORTHO
matériau orthotrope

EX=ex, EY=ey, EZ=ez, NUXY=uxy,... DEN=r, AX=ax, ...;

 EX=ex_réel
EY=ex_réel
EZ=ez_réel

modules d'élasticité dans les directions X, Y, Z (Modulus of elasticity )

NUXY=nxy_réel
NUYZ=nyz_réel
NUXZ=nxz_réel

coefficients de Poisson XZ (Poisson's ratio)

GXY=gxz_réel
GYZ=gyz_réel
GXZ=gxz_réel

modules de cisaillement (Shear Modulus)
La loi de comportement d'un matériau élastique orthotrope est rappelée ci-dessous:

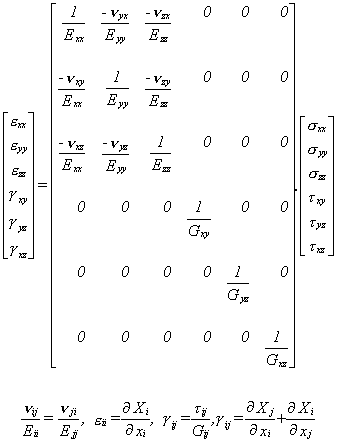
DEN=den_réel

densité massique (Mass density)

AX=ax_réel

AY=ay_réel

AY=az_réel

                coefficients de dilatation thermique en X, Y et Z (Coefficient of thermal expansion)

TREF=

température de référence (Thermal expansion reference) temperature

 GE=ge_réel

amortissement structurel (Structural element damping coefficient)

KX=kx_réel
KY=ky_réel
KZ=kz_rée

conductivités thermiques en X, Y et Z (Thermal conductivity)

Q=q_réel

taux de génération de chaleur (Heat Generation rate)

CF=cf_réel

convection thermique (convective film coefficient)

HF=hf_réel

taux d'émission de chaleur (Heat flux rate)

SHF=s_réel

taux d'émission de chaleur surfacique (Surface Heat flux rate)

CP=cp_réel

chaleur spécifique (Specific heat)

V=m_réel

                viscosité (viscosity)

MU=h_réel

coefficient de friction (coefficient of friction)

SCX=scxréel

coefficient de gonflement en X (Swelling coefficient in X)

SCY=scyréel

coefficient de gonflement en Y (Swelling coefficient in Y)

XT=s1+réel

contrainte en traction X (Allowable stress in tension in X direction)

XC=s1-réel

contrainte en compression X (Allowable stress in compression in X direction)

YT=s2+réel

contrainte en traction X (Allowable stress in tension in Y direction)

YC=s2-réel

contrainte en compression X (Allowable stress in compression in Y direction)

S=t0réel

contrainte en cisaillement plan (Allowable in-plane shear stress)

F12=f12réel

terme d'interaction pour le critère de Tsai-Wu (Interaction term for Tsai-Wu)
Un matériau soumis à un état de contrainte plane ne subit pas de ruine selon le critère de  Tsai-Wu lorsque:

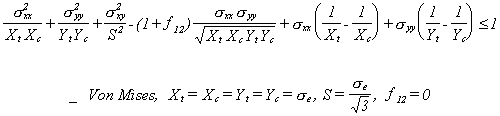
Ce critère est une généralisation du critère de Von Mises applicable aux matériaux isotropes.

TYPE=ANISO
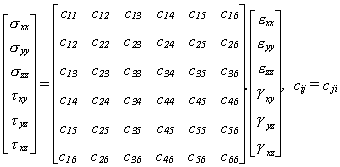
matériau anisotrope

RW1=c11,c12,c13,c14,c15,c16, RW2=c22,c23,c24,c25,c26, ..., RW6=c66, ...;

RW1=c11, c12, c13, c14, c15, c16

coefficients de la première ligne de la matrice d'élasticité.

RW2=c22, c23, c24, c25, c26

coefficients de la deuxième ligne de la matrice d'élasticité.

RW3=c33, c34, c35, c36

coefficients de la troisième ligne de la matrice d'élasticité.

RW4= c44, c45, c46

coefficients de la quatrième ligne de la matrice d'élasticité.

RW5= c55, c56

coefficients de la cinquième ligne de la matrice d'élasticité.

RW6= c66

coefficient de la sixième ligne de la matrice d'élasticité.
La loi de comportement d'un matériau élastique anisotrope est rappelée ci-dessous:

TEV=a1, a2, a3, a4, a5, a5

Vecteur des coefficients de dilatation thermique (Thermal Expansion Vector)

KKM=k1, k2, k3, k4, k5, k5

Matrice de conductivité thermique (thermal conductivity Matrix)

GE=ge, DEN=_, CP=cp, XT=s1+, XC=s1-, YT=s2+, YC=s2-,S=t0, F12=f12, SCX=scx, SCY=scy

Les définitions de ces paramètres sont identiques à celles données pour l'entité: PROPERTY(TYPE=ORTHO)

TYPE=LAMINATE
matériau composite

M=m11,m12,m13,m22,m23,m33, ...;

M=m11, m12, m13, m22, m23, m33

coefficients de rigidité de membrane.

B=b11, b12, b13, b22, b23, b33

coefficients de rigidité de flexion.

C=c11, c12, c13, c22, c23, c33

coefficients de rigidité de couplage membrane-flexion.

S=s11, s12, s22

coefficients de rigidité de cisaillement transverse

LTK=h

épaisseur du composite.

La loi de comportement d'un matériau composite est rappelée ci-dessous:

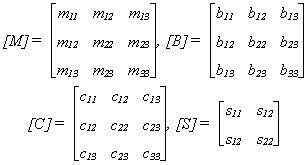
TYPE=BEAM_LINEAR
propriétés physiques pour poutres de section constante

AR=ar, IYY=iyy, ..., SRY=sry;

AR=ar_réel

section de la poutre (Area, m2)

IYY=iyy_réel
IZZ=izz_réel

Moments d'inertie Y et  Z (Moment of inertia, m4). Les définitions de ces coefficients sont rappelées ci-après:

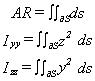
Le moment d'inertie Iyy  est relatif à des rotations autour de l'axe (y) de la poutre (donc pour des moments fléchissants Myy et des efforts tranchants Tz). Ce coefficient Iyy intervient pour une flexion de la poutre soumise à une charge répartie orientée dans la direction (z) du repère local de la poutre.

TC=tc_réel

constante de torsion (Torsional constant, m4)

SRY=sry_réel
SRZ=srz_réel

coefficients de correction pour la prise en compte du cisaillement transverse dans les directions du repère local de la poutre Y et Z.  (Shear area Ratio Y,Z). Le coefficient <srz> est relatif aux chargements dans le plan (xz) de la poutre et va donc affecter le calcul des moments fléchissants Myy.

TKY=tky_réel
TKZ=tkz_réel

épaisseurs de la section dans les directions Y et Z du repère local de la poutre (unité SI : m).

IVY=(I/v)yréel
IVZ=(I/v)zréel

Ces coefficients sont employés pour les calculs de contraintes normales à la section de la poutre en flexion. Si la poutre est soumise à un pur moment fléchissant Myy, alors les contraintes sxx dans la section de la poutre sont telles que |sxx| £ |Myy|/(I/v)y.
Pour un pur moment fléchissant Mzz, nous avons |sxx| £ |Mzz|/(I/v)z. (unité SI : m3)

ITC=(J/r)réel

Ce coefficient est employé pour les calculs de contraintes de cisaillement associées à une torsion. Si la poutre est soumise à un pur moment de torsion Mxx, alors les contraintes de cisaillement t dans la section de la poutre sont telles que |t| £ |Mxx|/(J/r)  (unité SI : m3).

ARY=aryréel
ARZ=arzréel

Ces coefficients sont employés pour les calculs de contraintes de cisaillement lorsque la poutre est soumise à des efforts tranchants: ty=Ty/ary, tz=Tz/arz. (unité SI : m2).

EA=earéel

Epaisseur de l'âme pour les poutres en I. Ce coefficient sert au calcul du critère de voilement (unité SI : m).

LKY=Lky_réel
LKZ=Lkz_réel

Longueurs minimales de flambement (Lky concernant la rotation autour de l'axe yy, c'est-à-dire pour une flexion créée par un effort tranchant Tz). Si les longueurs de la poutre est inférieure à Lky, la longueur de flambement dans le plan XZ est Lky.
NB: si LKZ est indiqué et si LKY=0, alors LKY est égal à LKZ.

LDY=Ldy_réel
LDZ=Ldz_réel 

Longueurs minimales de déversement.

SP=S_réel

Moment statique relatif à des moments autour de l'axe (y). Le moment statique permet de tenir compte de la plastification de la poutre dans les critères de ruine de constructions métalliques avec le coefficient y=2S/(Iyy/v). (unité SI : m3)

CFI=c0réel

coût fixe de chaque poutre.

CVA=c1réel

coût par unité de longueur de chaque poutre. Le coût d'utilisation d'une poutre est: c=c0+c1xL, où L est la longueur de la poutre.

Remarque 1: Le repère local de chaque poutre est défini dans l'entité "ELEMENT(TYPE=BEAM_LINEAR)"

NCM=Nx_créel

Effort de compression maximum admissible

NTM=Nx_tréel

Effort de traction maximum admissible

NX=Nxréel

Tension initiale de précontrainte

MYA=-My1réel

Moment Myy initial de précontrainte à l'extrémité 1

MYB=-My2réel

                Moment Myy initial de précontrainte à l'extrémité 2

MZA=Mz1réel

Moment Mzz initial de précontrainte à l'extrémité 1

MZB=Mz2réel

Moment Mzz initial de précontrainte à l'extrémité 2

IXY=product of inertia

ECY=

Eccentricity Y

ECZ=

Eccentricity Z

ECZ=

Eccentricity Z

TKZ=Thickness Z

TKY=Thickness Y

IS=Initial strain

WC=Warping coefficient

BOC=entier

Beam orientation code

BOS=[3]

Beam orientation specification

RFE=entier

Release (fore end)

SFE=[6]

Springs (fore end)

RFA=entier

Release (aft end)

SFA=[6]

Springs (aft end)

OFCF=entier

Offset code (fore end)

OFCA=entier

Offset code (aft end)

OFVF=[3]Offset vector (fore end)

OFVA=[3]Offset vector (aft end)

SRC=[2]Stress recovery C

ERTC=Effective radius in torsion C

SRD=[2]Stress recovery D

ERTD=Effective radius in torsion D

SRE=[2]Stress recovery E

ERTE=Effective radius in torsion E

SRF=[2]Stress recovery F

ERTF=Effective radius in torsion F

NSML=Nonstructural mass per unit length

FIX=Degree of fixity

CSC=entierCombined stress code

SAL=Surface area per unit length

TYPE=BEAM_TAPERED
propriétés physiques pour poutres de section variable

Les sections de ces poutres varient linéairement entre l'origine (notée 1) et l'extrémité (notée 2). Les propriétés sont identiques à celles des poutres de type BEAM_LINEAR mais définies 2 fois, à l'origine et à l'extrémité, pour les valeurs AR, IYY, IZZ, SRY, SRZ, ITC, SP, EA.

Les dimensions de la poutre sont définies par:

TYT: "demi"-largeur dans la direction Y+
TYB: "demi"-largeur dans la direction Y-
TZT: "demi"-hauteur dans la direction Z+
TZB: "demi"-hauteur dans la direction Z-

TYPE=BUSHING
propriétés physiques pour silentblocs (appui élastique)

K=kx, ky, kz, krx, kry, krz;

K=kx_réel, ky, kz, krx, kry, krz
Kij=k_{réel (1<=i<=6, i<=j<=6, [v5.2])}

rigidités  (N/m pour kx, ky, kz), (N.m/rad pour krx, kry, krz).

Un appui élastique "BUSHING" (cf entité ELEMENT(TYPE=BUSHING) est assimilable à une barre rigide entre les noeuds <n1,n1'> associée à une élasticicté [K] localisée à l'extrémité de cette barre entre les noeuds <n1',n2>. <n1> est le premier noeud, <n2> le deuxième noeud, <n1'> est un noeud fictif localisé au même emplacement que <n2> si l'appui ne subit aucune déformation.

Nous notons F1 le torseur force associé au noeud <n1'> dans le repère local de l'élément "BUSHING" ayant pour composantes (Fx1, Fy1, Fz1, Mx1, My1, Mz1) et D1 le vecteur des déplacements et des rotations du noeud n1'. Nous adoptons des notations analogues pour le deuxième noeud <n2> (F2, D2). Les relations établies par l'élément "BUSHING" sont les suivantes:

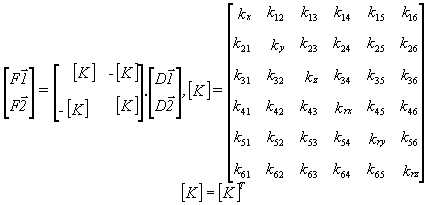
NB : la matrice [K] est symétrique et seuls les termes diagonaux et triangulaires supérieurs (j>= i) sont indiqués. Les indices utilisés sont: 1 pour la translation X (2=Y, 3=Z), 4 pour la rotation RX (5=RY, 6=RZ).

CFI=c0_réel
                coût fixe de chaque silentbloc.

TYPE=MASS
propriétés physique d'une masse

MA=mass, MIM=jxx, jyy, jzz, jxy, jxz, jyz;

MA=mass_réel

Masse (unité SI: kg)

MIM=jxx_réel, jyy_réel, jzz_réel,  jxy_réel,  jxz_réel, jyz_réel

                Matrice d'inertie (unité SI: kg.m2):

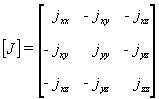
MICS=entier
Mass inertia coordinate system        

MOCS=entier
Mass offset code

MO=[3]Mass offsets

C1=entier
Component number 1

MAX=MassX
MAY=MassY
MAZ=MassZ

MAR1=[6]Row 1 mass matrix
MAR2=[6]Row 2 mass matrix
MAR3=[6]Row 3 mass matrix
MAR4=[6]Row 4 mass matrix
MAR5=[6]Row 5 mass matrix
MAR6=[6]Row 6 mass matrix

CFI=c0_réel
                coût fixe de chaque masse.

TYPE=ROD

propriété physique des  barres élastiques

AR=ar;

AR=ar_réel

section de la poutre (Area, m2)

CFI=c0_réel

coût fixe de chaque barre.

CVA=c1_réel

coût par unité de longueur de chaque barre. Le coût d'utilisation d'une barre est: c=c0+c1xL, où L est la longueur de la barre.

Remarque: Le type de matériau doit être indiqué dans une entité PROPERTY(TYPE=ISO).
Il est déconseillé d'utiliser le type de propriété ROD, hormis pour les câbles, préférez plutôt le type BEAM_LINEAR;
en effet, un élément de type ROD, peut utiliser des propriétés de type BEAM_LINEAR, ce qui permet de vérifier le flambement de cette barre.

TYPE=SPRING

propriétés physiques pour ressorts.

K=k, MA=mass;

K=k_réel

rigidité du ressort (N/m = kg.s-2).

MAF=mass_réel

masse du ressort (kg).

CFI=c0_réel

coût fixe de chaque ressort.

TYPE=SHELL

propriétés physiques pour coques.

TK=h;

TK=h_réel

épaisseur de la coque (m).
Ce paramètre n'est employé que lorsque la coque est constituée d'un matériau isotrope ou orthotrope. Pour les coques composites, reportez-vous à l'entité PROPERTY(TYPE=LAMINATE).

/*      caractéristiques d'un matériau isotrope */
PROPERTY(TYPE=ISO)
steel;          E=210.0E9, NU=0.3, DEN=7.8E3;

/*       propriétés physiques pour poutre               */
PROPERTY(TYPE=BEAM_LINEAR)
beam1;  AR=1.0E-3, IYY=2.0E-7, IZZ=1.6E-7, TC=3.2E-7;

/*      masse ponctuelle de 15.1 avec comme matrice d'inertie
*       Jxx=1.1, Jyy=1.3, Jzz=1.1, Jxy=0.3, Jyz=0.1, Jxz=0.2
*/
PROPERTY(TYPE=MASS)
mass1;  MA=15.1, MIM=1.1, 1.3, 1.1, 0.3, 0.1, 0.2;

/*      exemple de définition de propriété physique
*       avec la référence à un matériau par défaut
*       (matériau "steel", défini dans le premier exemple ci-dessus)
*/
PROPERTY(TYPE=ROD, MAT=steel)
bar1;   AR=1.0E-3;

/*      ainsi, si un élément barre de type "ROD" utilise la propriété "PROP=bar1"
*       sans indiquer un matériau, alors le matériau utilisé est "steel"
*       exemple:
*/

ELEMENT(TYPE=ROD, PROP=bar1)
el1;    N1,     N2;

/*      élément poutre utilisant "beam1" et "steel"     */
ELEMENT(TYPE=BEAM_LINEAR, PROP=beam1, MAT=steel)
el2;    N3,     N4,     N5;